Diagonals of a Rectangle Are of Equal Length
Diagonals of a Rectangle Are of Equal Length
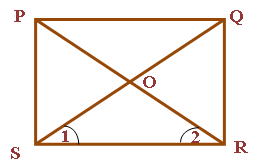
Theorem 2: The diagonals of a rectangle are of equal length.
Given : PQRS is a rectangle. To Prove : PR = QS Proof:As each rectangle is a parallelogram and PQRS is a rectangle Therefore PQRS is a parallelogram PS = QR '................(1) [ Opposite sides of a parallelogram] As each angle of a rectangle is a right angle In PS = QR [ From Equation 1 ] RS = RS [ Common ]
Hence Proved |  |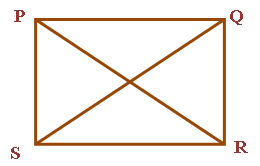
Converse of Theorem 2: If the diagonals of a parallelogram are of equal length, it is a rectangle.
Given : PQRS is a parallelogram such that PR = QS. To Prove : PQRS is a rectangle Proof: In PR = QS [ Given ] PS = QR [ Opposite sides of parallelogram ] RS = RS [ Common ]
As PQRS is a parallelogram, PS || QR Now PS || QR and RS is the transversal
Now PQRS is a parallelogram in which one angle is a right angle. Therefore PQRS is a rectangle Hence Proved | |
Illustration: The diagonals of a rectangle PQRS intersect at O, If
Solution: PQRS is a rectangle and we know that diagonals of a rectangle are equal Each rectangle is aparallelogram and we know that diagonals of a parallelogram bisect each other Therefore OS = OR [ Because when diagonals are equal halves are equal ] In
Now
Now each angle of a rectangle is a right angle. |
|
ABCD is a rectangle with | |||
| Right Option : A | |||
| View Explanation | |||
The diagonals of a rectangle PQRS intersect at O, If | |||
| Right Option : B | |||
| View Explanation | |||
The diagonals of a rectangle PQRS intersect at O, If | |||
| Right Option : B | |||
| View Explanation | |||
Students / Parents Reviews [10]
I have spent a wonderful time in Abhyas academy. It has made my reasoning more apt, English more stronger and Maths an interesting subject for me. It has given me a habbit of self studying
Yatharthi Sharma
10thAbhyas Methodology is very good. It is based on according to student and each child manages accordingly to its properly. Methodology has improved the abilities of students to shine them in future.
Manish Kumar
10thIt was a good experience with Abhyas Academy. I even faced problems in starting but slowly and steadily overcomed. Especially reasoning classes helped me a lot.
Cheshta
10thMy experience with Abhyas academy is very good. I did not think that my every subject coming here will be so strong. The main thing is that the online tests had made me learn here more things.
Hiya Gupta
8thOne of the best institutes to develope a child interest in studies.Provides SST and English knowledge also unlike other institutes. Teachers are co operative and friendly online tests andPPT develope practical knowledge also.
Aman Kumar Shrivastava
10thBeing a parent, I saw my daughter improvement in her studies by seeing a good result in all day to day compititive exam TMO, NSO, IEO etc and as well as studies. I have got a fruitful result from my daughter.
Prisha Gupta
8thIt was good as the experience because as we had come here we had been improved in a such envirnment created here.Extra is taught which is beneficial for future.
Eshan Arora
8thAbout Abhyas metholodology the teachers are very nice and hardworking toward students.The Centre Head Mrs Anu Sethi is also a brilliant teacher.Abhyas has taught me how to overcome problems and has always taken my doubts and suppoeted me.
Shreya Shrivastava
8thA marvelous experience with Abhyas. I am glad to share that my ward has achieved more than enough at the Ambala ABHYAS centre. Years have passed on and more and more he has gained. May the centre flourish and develop day by day by the grace of God.
Archit Segal
7thMy experience with Abhyas is very good. I have learnt many things here like vedic maths and reasoning also. Teachers here first take our doubts and then there are assignments to verify our weak points.
